pytorch
41 minutes read (About 6105 words)

pytorch学习

Introduction to Neural Network

在人工神经网络里，没有产生新连接，网络固定不变

反向传播: 对比预测答案和真实答案的差别，再将差别去 反向传播 调整参数，提高正确率

详细的训练: 每个神经元都有一个自己的activate function, 刺激行为

神经网络: 梯度下降公式-》 优化问题optimization

求导求微分，Gradient Descent

image-20190815204001644

沿着梯度去下降，得到最小的W值 -> 优化问题

迁移学习: 拆掉输出层，保留分辨能力，添加其他层，进行另外的功能

Pytorch

PyTorch 是 Torch 在 Python 上的衍生. 因为 PyTorch 是一个使用 PyTorch 语言的神经网络库, Torch 很好用, 但是 Lua 又不是特别流行, 所有开发团队将 Lua 的 Torch 移植到了更流行的语言 Python 上. 是的 PyTorch 一出生就引来了剧烈的反响. 为什么呢?

而且如果你知道 Numpy, PyTorch 说他就是在神经网络领域可以用来替换 numpy 的模块.

神经网络在做什么

神经网络在学习拟合线条(回归):

Why Pytorch?

PyTorch 和 Tensorflow

据 PyTorch 自己介绍, 他们家的最大优点就是建立的神经网络是动态的, 对比静态的 Tensorflow, 他能更有效地处理一些问题, 比如说 RNN 变化时间长度的输出. 而我认为, 各家有各家的优势和劣势, 所以我们要以中立的态度. 两者都是大公司, Tensorflow 自己说自己在分布式训练上下了很大的功夫, 那我就默认 Tensorflow 在这一点上要超出 PyTorch, 但是 Tensorflow 的静态计算图使得他在 RNN 上有一点点被动 (虽然它用其他途径解决了), 不过用 PyTorch 的时候, 你会对这种动态的 RNN 有更好的理解.

Torch 或 Numpy

Torch 自称为神经网络界的 Numpy, 因为他能将 torch 产生的 tensor 放在 GPU 中加速运算 (前提是你有合适的 GPU), 就像 Numpy 会把 array 放在 CPU 中加速运算. 所以神经网络的话, 当然是用 Torch 的 tensor 形式数据最好咯. 就像 Tensorflow 当中的 tensor 一样.

1
2
3
4
5
6
7
import torch
import numpy as np
np_data = np.arange(6).reshape((2, 3))
torch_data = torch.from_numpy(np_data)
tensor2array = torch_data.numpy()

np.sin(data) == torch.sin(data)

除了简单的计算, 矩阵运算才是神经网络中最重要的部分. 所以我们展示下矩阵的乘法. 注意一下包含了一个 numpy 中可行, 但是 torch 中不可行的方式.

variable就是存放神经网络参数的东西，并且神经网络优化一般都是优化类型为variable的节点

1
2
3
4
5
6
7
8
9
# matrix multiplication 矩阵点乘
data = [[1, 2], [3, 4]]
tensor = torch.FloatTensor(data)
# correct method
print(
    "\nmatrix multiplication (matmul)",
    "\nnumpy", np.matmul(data, data),
    "\ntorch", torch.mm(tensor, tensor)
)

变量 (Variable)

在 Torch 中的 Variable 就是一个存放会变化的值的地理位置. 里面的值会不停的变化. 就像一个裝鸡蛋的篮子, 鸡蛋数会不停变动. 那谁是里面的鸡蛋呢, 自然就是 Torch 的 Tensor 咯. 如果用一个 Variable 进行计算, 那返回的也是一个同类型的 Variable.

我们定义一个 Variable:

1
2
3
4
5
6
7
8
9
10
import torch
from torch.autograd import Variable  # torch 中 Variable模块
# 先 生鸡蛋
tensor = torch.FloatTensor([[1, 2], [3, 4]])
# 把鸡蛋 放到篮子中， require_grad是参不参与误差反向传播,要不要计算梯度
variable = Variable(tensor, requires_grad = True)

print(
	tensor
)

Variable 计算, 梯度

我们再对比下Tensor的计算和variable的计算

1
2
3
4
5
6
7
import torch
from torch.autograd import Variable
tensor = torch.FloatTensor([[1, 2], [3, 4]])
t_out = torch.mean(tensor*tensor)
v_out = torch.mean(variable*variable)
print(t_out) # 7.5
print(v_out) # 7.5

到目前为止, 我们看不出什么不同, 但是时刻记住, Variable 计算时, 它在背景幕布后面一步步默默地搭建着一个庞大的系统, 叫做计算图, computational graph. 这个图是用来干嘛的? 原来是将所有的计算步骤 (节点) 都连接起来, 最后进行误差反向传递的时候, 一次性将所有 variable 里面的修改幅度 (梯度) 都计算出来, 而 tensor 就没有这个能力啦.

v_out = torch.mean(variable*variable) 就是在计算图中添加的一个计算步骤, 计算误差反向传递的时候有他一份功劳, 我们就来举个例子:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import torch 
from torch.autograd import Variable # 导入 Variable 模块
tensor = torch.FloatTensor([[1, 2], [3, 4]]) 
variable = Variable(tensor, requires_grad = True)

t_out = torch.mean(tensor*tensor)
v_out = torch.mean(variable*variable)
print(t_out)
print(v_out)

v_out.backward()  # 模拟v_out误差反向传播
# Variable是计算图是的一部分
# v_out 是 1/4 * sum(variable*variable) 这是计算图中的 v_out 计算步骤
# 针对 v_out 的梯度是 d(v_out)/d(variable) = 1/2 * variable

# 初始化的梯度
print(
    "variable.grad: ",variable.grad
)

获取Variable 里面的数据

直接print(variable)只会输出Variable 形式的数据，很多时候用不了(plt画图)，转化成Tensor

1
2
3
print(variable) # Variable 形式
print(Variable.data) # tensor 形式
print(variable.data.numpy()) # numpy形式

激励函数 Activation Function

为什么需要？解决 日常生活总不能用 线性方程解决的问题

Linear; NonLinear; y = Wx => y = AF(Wx) ; W 就是我们要求的参数, y 是预测值, x 是输入值.

image-20190817100050191

激励函数

image-20190817100706478

AF 就是指的激励函数(本身就是非线性的，必须可微分). 激励函数拿出自己最擅长的”掰弯利器”, 套在了原函数上 用力一扭, 原来的 Wx 结果就被扭弯了。

你甚至可以创造自己的激励函数来处理自己的问题, 不过要确保的是这些激励函数必须是可以微分的, 因为在 backpropagation 误差反向传递的时候, 只有这些可微分的激励函数才能把误差传递回去。当你使用特别多层的神经网络, 在掰弯的时候, 玩玩不得随意选择利器. 因为这会涉及到梯度爆炸, 梯度消失的问题。卷积神经网络 Convolutional neural networks 的卷积层中, 推荐的激励函数是 relu. 在循环神经网络中 recurrent neural networks, 推荐的是 tanh 或者是 relu

pytorch activation function

激励函数 (./pytorch学习/6.png)

神经网络中的每一层出来都是线性的函数关系，而在日常生活许多都是非线性关系。因此我们需要用激活函数将线性网络转成非线性结果。就是让神经网络可以描述非线性问题的步骤, 是神经网络变得更强大.

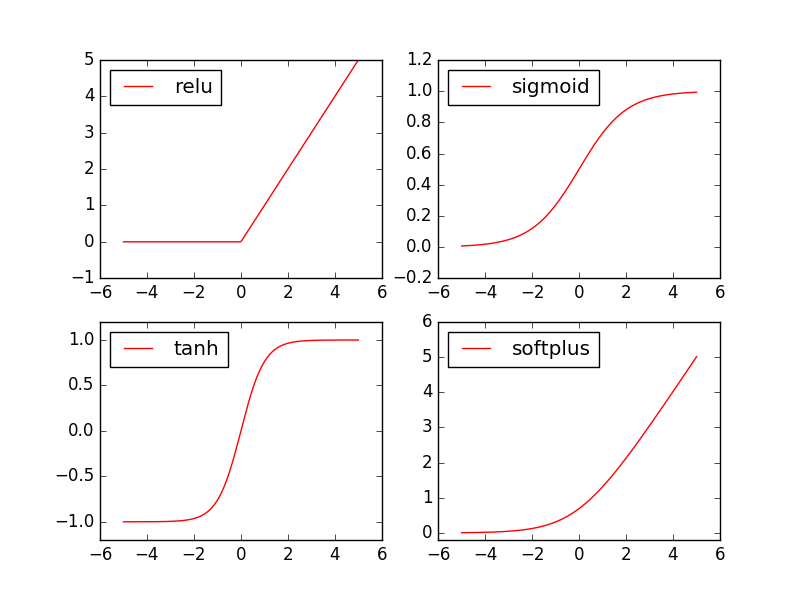
Torch中的激励函数

Torch中的激励函数: relu, sigmoid, tanh, softplus

1
2
3
4
5
6
import torch
import torch.nn.funcational as F # 激励函数在此
from torch.autograd import Variable
# 做数据
x = torch.linespace(-5, 5, 200)  # x data (Tensor), shape=(100, 1)
x = Variable(x)

接着就是做生成不同的激励函数数据:

1
2
3
4
5
6
7
x_np = x.data.numpy() # 换成 numpy, array,出图用
# 常用的 激励函数
y_relu = F.relu(x).data.numpy()  # 0 -> 
y_sigmoid = F.sigmoid(x).data.numpy() # 0 ~ 1
y_tanh = F.tanh(x).data.numpy() # -1 ~ 1
y_softplus = F.softplus(x).data.numpy() # 0 ~
# y_softmax = F.softmax(x) softmax 比较特殊， 不能直接显示，他是关于概率的，用于分类
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import matplotlib.pyplot as plt # python 的可视化模块

plt.figure(1, figsize = (8, 6))

plt.subplot(221)
plt.plot(x_np, y_relu, c='red', label="relu")
plt.ylim((-1, 5))
plt.legend(loc="best")

plt.subplot(223)
plt.plot(x_np, y_sigmoid, c="blue", label="sigmoid")
plt.ylim((-0.1, 1.2))
plt.legend(loc="best")

plt.subplot(222)
plt.plot(x_np, y_tanh, c="orange", label="tanh")
plt.ylim((-1.1, 1.1))
plt.legend(loc="best")

plt.subplot(224)
plt.plot(x_np, y_softplus, c="yellow", label="softplus")
plt.ylim((-1, 5))
plt.legend(loc="best")

plt.show()

image-20190817160302989

神经网络

神经网络分为两类: 回归和分类；

回归，就是结果为一些系列连续的值，如f(房价) = W(大小，地点等)；

分类，就是判断结果的类别， 如图像中判断 是 猫还是狗

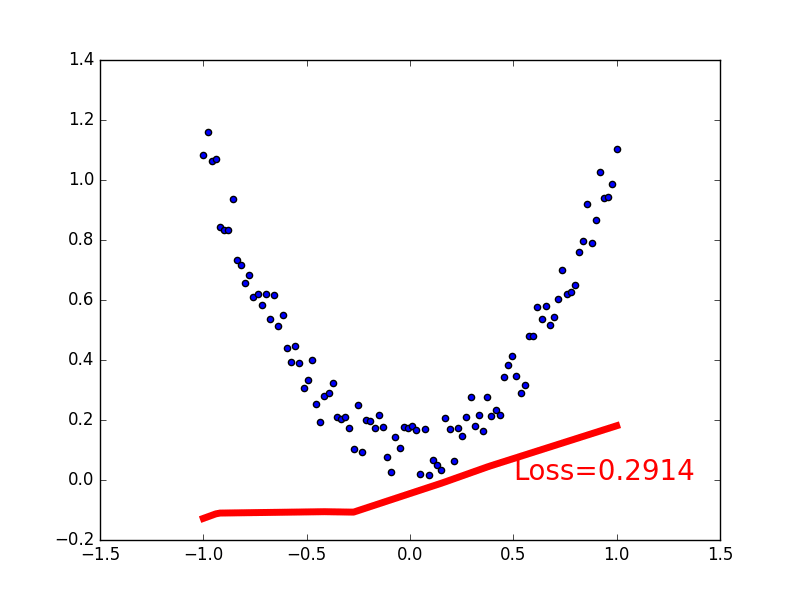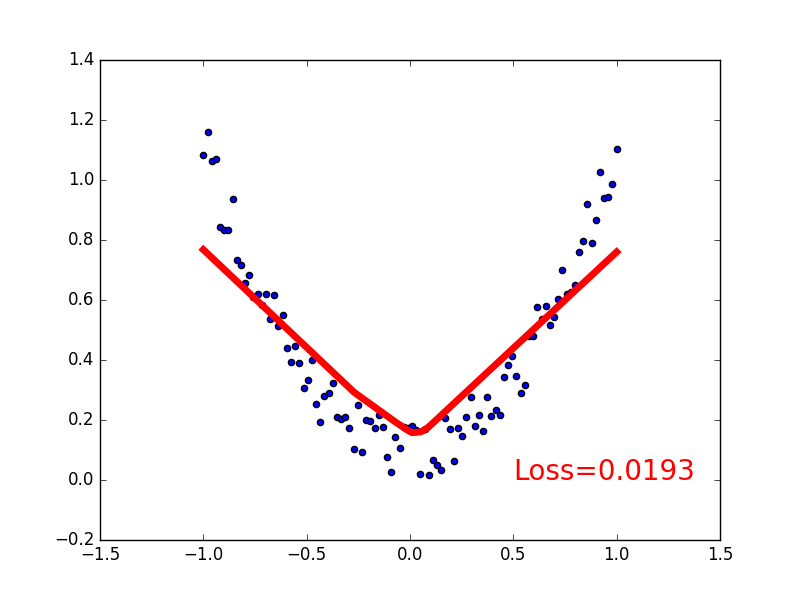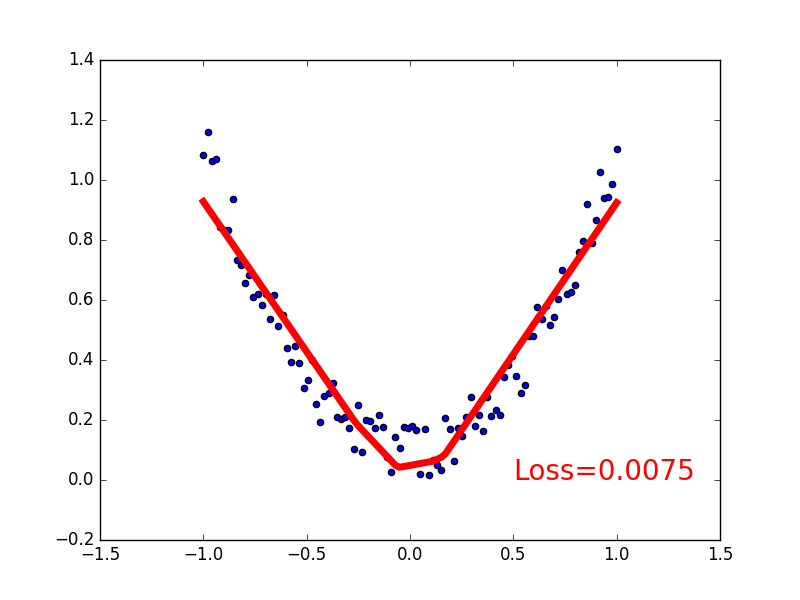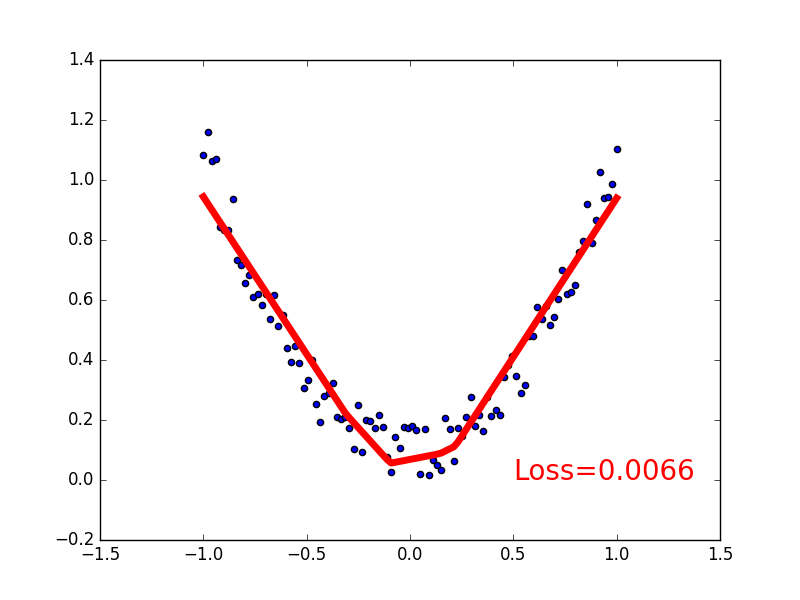
关系拟合(回归)

来见证神经网络是如何通过简单的形式将一群数据用一条线条来表示. 或者说, 是如何在数据当中找到他们的关系, 然后用神经网络模型来建立一个可以代表他们关系的线条.

建立数据集

我们创建一些假数据来模拟真实的情况. 比如一个一元二次函数: y = a * x^2 + b, 我们给 y 数据加上一点噪声来更加真实的展示它.

1
2
3
4
5
6
7
8
9
import torch
import matplotlib.pyplot as plt

x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # x data (tensor),shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size())  # nosiy y data (tensor), shape=(100, 1)

# 动画
plt.scatter(x.data.numpy(), y.data.numpy())
plt.show()

建立神经网络

建立一个神经网络我们可以直接运用 torch 中的体系. 先定义所有的层属性(__init__()), 然后再一层层搭建(forward(x))层与层的关系链接. 建立关系的时候, 我们会用到激励函数, 

1
2
3
4
5
6
7
8
9
10
import torch
import torch.nn.funcational as F

class Net(torch.nn.Module): # 1. 继承 torch 的Module  
		def __init__(self):   # 2. 初始化模块， 去继承， 搭建完成每层的定义，信息
      super(Net, self).__init__() # 2. 继承关系 __init__ 功能
      pass
    
    def forward(self, x):  # 3. 完成层与层之间的 forward的联系, 前向传播
      pass
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import torch
import torch.nn.funcational as F

class Net(torch.nn.Module): # 1. 继承 torch 的Module  
		def __init__(self, n_features, n_hidden, n_output):   # 2. 初始化模块， 去继承， 搭建完成每层的定义，信息; 神经元的个数
      super(Net, self).__init__() # 2. 继承关系 __init__ 功能
      # 4. 每一层的信息都是 模块的一个属性,属性的内容就是一层神经网络: 多少个输入，多少个输出，做什么操作
      # 4. 这是只是搭建了各层神经元的内容
      self.hidden = torch.nn.Linear(n_features, n_hidden)
      self.predict = torch.nn.Linear(n_hidden, n_output)
      pass
    
    def forward(self, x):  # 3. 完成层与层之间的 forward的联系, 前向传播流程
      # 5. 层与层之间的关系， 整个搭建过程，用激活函数激活
      # 正向传播输入值, 神经网络分析出输出值
      x = F.relu(self.hidden(x))
      x = self.predict(x)  # 输出层不需要用激活函数去截断
      return x
net = Net(n_features=1, n_hidden=10, n_output=1)
print(net)# net 的结构
"""
Net (
  (hidden): Linear (1 -> 10)
  (predict): Linear (10 -> 1)
)
"""

训练网络

训练步骤很简单:

1
2
3
4
5
6
7
8
9
10
11
# 设置 优化函数；设置 误差函数； 迭代训练: 喂数据给模型，计算得到 loss，更新梯度，参数优化
# optimizer 是训练工具 优化参数
optimizer = torch.optim.SGD(net.parameters(), lr=0.2) # 传入 net所有参数,学习率
loss_func = torch.nn.MSELoss() # 预测值和真实值的误差计算公式(均方差)回归 mean squre error； 分类: cross entropy
for t in range(100):
  prediction = net(x)  # 喂给 net 训练数据 x； 输出 预测值
  loss = loss_func(prediction, y)   # 计算 误差, 拿去反向传播
  
  optimizer.zero_grad()  # 清空上一步的残余更新参数值
  loss.backward()  # 误差反向传播，计算参数更新值
  optimizer.step()  # 用optimizer去优化 将参数更新到施加到 net 的parameters 上

可视化训练过程

理解如何训练

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import matplotlib.pyplot as plt
plt.ion()  # 画图
plt.show()

optimizer = torch.optim.SGD(net.parameters(), lr=0.2)
loss_func = torch.nn.MSELoss()
for t in range(200):
  prediction = net(x)
  loss = loss_func(prediction, y)  
  optimizer.zero_grad()
  loss.backward()
  optimizer.step()
  
  if t%5 == 0:
    # plt and show learning process
    plt.cla()
    plt.scatter(x.data.numpy(), y.data.numpy())
    plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
    plt.text(0.5, 0. "Loss=%.4f" % loss.data.numpy(), fontdict={'size': 20, 'color': 'red'})
    plt.pause(0.1)

区分类型(分类)

Classification 分类; x 是32bit FloatTensor, y 64bit FloatTensor

建立数据集

创建一些假数据来模拟真实的情况. 比如两个二次分布的数据, 不过他们的均值都不一样.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import torch
import matplotlib.pyplot as plt

# 模拟分类数据
n_data = torch.ones((100, 2))  # 数据基本形态， shape=(100, 2)
x0 = torch.normal(2*n_data, 1) # 类型 0 x (tensor), shape=(100,2)
y0 = torch.zeros((100,)) # y0 = torch.zeros((100, )) 类型 0 y data (tensor), shape=(100,)
x1 = torch.normal(-2*n_data, 1) # 类型 1 x data (tensor),shape=(100, 2)
y1 = torch.ones((100,)) # 类型1 y data (tensor),shape=(100,)
# pytorch的数据形式 
x = torch.cat((x0, x1), 0).type(torch.FloatTensor) # FloatTensor = 32-bit floating
y = torch.cat((y0, y1),).type(torch.LongTensor) # LongTensor = 64-bit integer
plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=y.data.numpy(), s=100, lw=0, cmap='RdYlGn')
plt.show()

image-20190818111523023

建立神经网络

建立一个神经网络我们可以直接运用 torch 中的体系:

  1. 先定义所有的层属性(__init__()) , 定义神经元个数
  2. 再一层层搭建(forward(x))层于层的关系链接.建立关系的时候, 我们会用到激励函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import torch
import torch.nn.functional as F # activation
class Net(torch.nn.Module):
  # 神经元的节点数
  def __init__(self, n_feature, n_hidden, n_output):
    super(Net, self).__init__() # 继承 __init__ 功能
    self.hidden = torch.nn.Linear(n_feature, n_hidden)
    self.predict = torch.nn.Linear(n_hidden, n_output)
    pass
  def forward(self, x)：
  	x = F.relu(self.hidden(x))
    x = self.predict(x)
    return x
# 初始化
net = Net(n_feature=2, n_hidden=10, n_output=2) # 几个类别就几个 output
print(net)

训练网络

用优化器 训练 网络参数；loss 反向传播

1
2
3
4
5
6
7
8
9
10
11
optimizer = torch.optim.SGD(net.parameters(), lr=0.02) # set up optimizer, 传入参数，学习率
# 算误差时，注意真实值！ 不是one-hot形式的， 而是1D Tensor，(batch,)
# 但是预测值是2D tensor (batch, n_classes)
loss_func = torch.nn.CrossEntropyLoss()
for t in range(100):
  out = net(x) # 喂给 net 训练数据 x, 输出分析值
  loss = loss_func(out, y)  # 计算两者的误差
  
  optimizer.zero_grad() # 清空上一步的残余更新参数值
  loss.backward() # 误差反向传播, 计算参数更新值 
  optimizer.step()  # 将参数更新值施加到 net 的 parameters 上

可视化训练过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import matplotlib.pyplot as plt
plt.ion()
plt.show()
optimizer = torch.optim.SGD(net.parameters(), lr=0.02)
loss_func = torch.nn.CrossEntropyLoss()
for t in range(100):
	out = net(x)
	loss = loss_func(out, y)
	optimizer.zero_grad()
	loss.backward()
	optimizer.step()
	if t%2 == 0:
		plt.cla()
		# 过了一道 softmax 的激励函数后的最大概率才是预测值
		prediction = torch.max(F.softmax(out), 1)[1]
		pred_y = prediction.data.numpy().squeeze()
		target_y = y.data.numpy()
    plt.scatter(x.data.numpy()[:,0], x.data.numpy()[:,1], c=pred_y, s=100, lw=0, cmap='RdYlGn')
    accuracy = sum(pred_y == target_y) /200
    plt.text(1.5, -4, 'Accuracy=%.2f'%accuracy, fontdict={'size':20, 'color':'red'})
    plt.pause(0.1)
plt.ioff() #停止画图
plt.show()

image-20190818145029869

快速搭建

之前的搭法

1
2
3
4
5
6
7
8
9
10
11
12
13
import torch
class Net(torch.nn.Module):
  def __init__(self, n_feature, n_hidden, n_output):
		super(Net, self).__init__()
    self.hidden = torch.nn.Linear(n_feature, n_hidden)
    self.output = torch.nn.Linear(n_hidden, n_output)
    pass
  def forward(self, x):
    x = F.relu(self.hidden(x))
    x = self.output(x)
    return x
net1 = Net(1, 10, 1)
print(net) # 这是我们用这种方式搭建的 net1

我们用 class 继承了一个 torch 中的神经网络结构, 然后对其进行了修改, 不过还有更快的一招, 用一句话就概括了上面所有的内容!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
net2 = torch.nn.Sequential( # Sequential 一层一层的积累神经层,激活函数也是一层神经
	torch.nn.Linear(1, 10),
	torch.nn.ReLU(), # 调用了类的构造方法
	torch.mm.Linear(10, 1)
)
print(net1)
"""
Net (
  (hidden): Linear (1 -> 10)
  (predict): Linear (10 -> 1)
)
"""
print(net2)
"""
Sequential (
  (0): Linear (1 -> 10)
  (1): ReLU ()
  (2): Linear (10 -> 1)
)
"""

我们会发现 net2 多显示了一些内容, 这是为什么呢? 原来他把激励函数也一同纳入进去了, 但是 net1 中, 激励函数实际上是在 forward() 功能中才被调用的. 这也就说明了, 相比 net2, net1 的好处就是, 你可以根据你的个人需要更加个性化你自己的前向传播过程, 比如(RNN). 不过如果你不需要七七八八的过程, 相信 net2 这种形式更适合你.

保存提取

训练好了一个模型, 我们当然想要保存它, 留到下次要用的时候直接提取直接用

保存

我们快速建造数据，搭建神经网络

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import torch
torch.manual_seed(1)
# fake data
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # x data (tensor),shape=(100, 1)
y = x.pow(2)+0.2*torch.rand(x.size()) # noisy y data (tensor), shape=(100, 1)

def save():
  # set up net
  net1 = torch.nn.Sequential(
  	torch.nn.Linear(1, 10),
    torch.nn.ReLu(),
    torch.nn.Linear(10, 1)
  )
  optimizer = torch.optim.SGD(net1.parameters(), lr=0.02)
  loss_func = torch.nn.MSELoss()
  # train
  for t in range(2000):
		prediction = net1(x)
    loss = loss_func(prediction, y)
    optimizer.zero_grad()
    loss.backkward()
    optimizer.step()
  #接下来我们有两种途径来保存
  torch.save(net1, 'net.pkl') # save entire net
  torch.save(net1.state_dict(), 'net_params.pkl') # 只保存网络中的参数(速度快，占内存少)
  # plot result
  prediction = net1(x)
  plt.figure(1, figsize=(10, 3))
  plt.subplot(131)
  plt.title('Net1')
  plt.scatter(x.data.numpy(), y.data.numpy())
  plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)

提取网络

提取整个神经网络, 网络大的时候可能会比较慢.

1
2
3
4
5
6
7
8
def restore_net():
	# restore entire net1 to net2
  net2 = torch.load('net.pkl')
  prediction = net2(x)
  plt.subplot(132)
  plt.title('Net2')
  plt.scatter(x.data.numpy(), y.data.numpy())
  plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)

只提取网络参数

提取所有的参数, 然后再放到你的新建网络中.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def restore_params():
	# set up net3
  net3 = torch.nn.Sequential(
  	torch.nn.Linear(1, 10)
    torch.nn.ReLU()
    torch.nn.Linear(10, 1)
  )
  # load parameters to net3
  net3.load_state_dict(torch.load('net_params.pkl'))
  prediction = net3(x)
  plt.subplot(133)
  plt.title('Net3')
  plt.scatter(x.data.numpy(), y.data.numpy())
  plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)

显示结果

1
2
3
4
5
6
7
# 保存 net1 (1. 整个网络, 2. 只有参数)
save()
# 提取整个网络
restore_net()
# 提取网络参数, 复制到新网络
restore_params()
plt.show()

保存提取

批训练

Torch中有个帮助整理数据结构，DataLoader，用来包装自己的数据，进行批训练，批训练途径:

DataLoader

DataLoader 是 torch 给你用来包装你的数据的工具. 所以你要讲自己的 (numpy array 或其他) 数据形式装换成 Tensor, 然后再放进这个包装器中. 使用 DataLoader 有什么好处呢? 就是他们帮你有效地迭代数据。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
, ximport torch
import torch.utils.data as Data
torch.manual_seed(1)

BATCH_SIZE = 5 # 批训练的数据个数
# produce dataloader: tensor -> dataset -> torch dataset -> dataloader
x = torch.linspace(1, 10, 10) # x data (torch tensor)
y = torch.linspace(10, 1, 10) # y data (torch tensor)
# 先转换成 torch 能识别的Dataset
torch_dataset = Data.TensorDataset(data_tensor=x, target_tensor=y)
# 把dataset 放入 DataLoder
loader = Data.DataLoader(
	dataset=torch_dataset, # torch TensorDataset format
  batch_size = BATCH_SIZE, # mini batch size/
  shuffle=True, # 打乱
  num_workers=2, # 多线程
)
for epoch in range(3):  # 训练所有 !整套! 数据 3 次
	for step, (batch_x, batch_y) in enumerate(loader): # 每一步 loader释放一小批数据来学习
    # 训练的地方
    
    # 打印数据
    print('Epoch: ', epoch, '| Step: ', step, '| batch x: ', batch_x.numpy(), '| batch y: ', batch_y.numpy())

可以看出, 每步都导出了5个数据进行学习. 然后每个 epoch 的导出数据都是先打乱了以后再导出.

真正方便的还不是这点. 如果我们改变一下 BATCH_SIZE = 8, 这样我们就知道, step=0 会导出8个数据, 但是, step=1 时数据库中的数据不够 8个, 这时怎么办呢:

这时, 在 step=1 就只给你返回这个 epoch 中剩下的数据就好了.

加速神经网络训练 (Speed Up Training)

包括以下几种模式:

  • Stochastic Gradient Descent (SGD)
  • Momentum
  • AdaGrad
  • RMSProp
  • Adam

Stochastic Gradient Descent (SGD)

image-20190818163344387

最基础的方法就是 SGD 啦, 想像红色方块是我们要训练的 data, 如果用普通的训练方法, 就需要重复不断的把整套数据放入神经网络 NN训练, 这样消耗的计算资源会很大.

我们换一种思路, 如果把这些数据拆分成小批小批的, 然后再分批不断放入 NN 中计算, 这就是我们常说的 SGD 的正确打开方式了. 每次使用批数据, 虽然不能反映整体数据的情况, 不过却很大程度上加速了 NN 的训练过程, 而且也不会丢失太多准确率.如果运用上了 SGD, 你还是嫌训练速度慢, 那怎么办?

image-20190818163501734

事实证明, SGD 并不是最快速的训练方法, 红色的线是 SGD, 但它到达学习目标的时间是在这些方法中最长的一种. 我们还有很多其他的途径来加速训练.

Momentum 更新方法

image-20190818163532768

大多数其他途径是在更新神经网络参数那一步上动动手脚. 传统的参数 W 的更新是把原始的 W 累加上一个负的学习率(learning rate) 乘以校正值 (dx).这种方法可能会让学习过程曲折无比, 看起来像 喝醉的人回家时, 摇摇晃晃走了很多弯路.

image-20190818163647605

所以我们把这个人从平地上放到了一个斜坡上, 只要他往下坡的方向走一点点, 由于向下的惯性, 他不自觉地就一直往下走, 走的弯路也变少了. 这就是 Momentum 参数更新. 另外一种加速方法叫AdaGrad.

AdaGrad 更新方法

image-20190818163807844

这种方法是在学习率上面动手脚, 使得每一个参数更新都会有自己与众不同的学习率, 他的作用和 momentum 类似, 不过不是给喝醉酒的人安排另一个下坡, 而是给他一双不好走路的鞋子, 使得他一摇晃着走路就脚疼, 鞋子成为了走弯路的阻力, 逼着他往前直着走. 他的数学形式是这样的. 接下来又有什么方法呢? 如果把下坡和不好走路的鞋子合并起来, 是不是更好呢? 没错, 这样我们就有了 RMSProp 更新方法.

RMSProp 更新方法

image-20190818163916576

有了 momentum 的惯性原则 , 加上 adagrad 的对错误方向的阻力, 我们就能合并成这样. 让 RMSProp同时具备他们两种方法的优势. 不过细心的同学们肯定看出来了, 似乎在 RMSProp 中少了些什么. 原来是我们还没把 Momentum合并完全, RMSProp 还缺少了 momentum 中的 这一部分. 所以, 我们在 Adam 方法中补上了这种想法.

Adam 更新方法

image-20190818163958622

计算m 时有 momentum 下坡的属性, 计算 v 时有 adagrad 阻力的属性, 然后再更新参数时 把 m 和 V 都考虑进去. 实验证明, 大多数时候, 使用 adam 都能又快又好的达到目标, 迅速收敛. 所以说, 在加速神经网络训练的时候, 一个下坡, 一双破鞋子, 功不可没.

Optimizer 优化器

伪数据

为了对比各种优化器的效果, 我们需要有一些数据, 今天我们还是自己编一些伪数据, 这批数据是这样的:

image-20190818171449118

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import torch
import torch.utils.data as Data
import torch.nn.functional as F
import matplotlib.pyplot as plt
torch.manual_seed(1) # 使每次随机产生的数一样
LR = 0.01
BATCH_SIZE = 32
EPOCH = 12
# fake data
x = torch.unsqueeze(torch.linpsace(-1, 1, 1000), dim=1)
y = x.pow(2) + 0.1*torch.normal(torch.zeros(*x.size()))
# plot dataset
plt.scatter(x.numpy(), y.numpy())
plt.show()
# 使用上节提到 data loader: x,y -> torch dataset -> data loader
torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(dataset=torch_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2)

每个优化器优化一个神经网络

为了对比每一种优化器, 我们给他们各自创建一个神经网络, 但这个神经网络都来自同一个 Net 形式.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 默认的 network 形式
class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(1, 20)   # hidden layer
        self.predict = torch.nn.Linear(20, 1)   # output layer

    def forward(self, x):
        x = F.relu(self.hidden(x))      # activation function for hidden layer
        x = self.predict(x)             # linear output
        return x

# 为每个优化器创建一个 net
net_SGD         = Net()
net_Momentum    = Net()
net_RMSprop     = Net()
net_Adam        = Net()
nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam]

优化器 Optimizer

接下来在创建不同的优化器, 用来训练不同的网络. 并创建一个 loss_func 用来计算误差. 我们用几种常见的优化器, SGD, Momentum, RMSprop, Adam.

1
2
3
4
5
6
7
8
# different optimizers
opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR)
opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
opt_Adam = torch.optim.Adam(net.net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam]
loss_func = torch.nn.MSELoss()
loss_his = [[], [], [], []] # 记录 training 时不同神经网络的 loss

训练/出图

1
2
3
4
5
6
7
8
9
10
11
for epoch in range(EPOCH):
  print(epoch)
  for step, (b_x, b_y) in enumerate(loader):
    # 对每个优化器, 优化属于他的神经网络
    for net, opt, l_his in zip(nets, optimizers, loss_his):
      output = net(b_x)  # get output for every net
      loss = loss_func(output, b_y) # compute loss for every net
      opt.zero_grad() # clear gradients for next train
      loss.backward() # backpropagation, compute gradients
      opt.step() # apply gradients
      l_his.append(loss.data.numpy()) # loss recoder
# pytorch学习
yaml入门
Golang总结
SEGUIR

Links

Categorias

Nube de etiquetas

AI BigData C++ Cryptography Federated Learning Goa入门 Java LeetCode Leetcode Mac终端命令 Swagger coding data encryption github golang hexo important intro npm paper paper reading paperReading python转换 pytorch学习 云端学习笔记 代码 入门 入门指引 刷题 双指针 基础 大数据，spark 排序 提升自我 深度学习 神经网络搜索 禅 编程 编程技巧， 联合学习 自我修炼 论文阅读 配置文件

Recientes

Archivos

Etiquetas

AI 1
BigData 1
C++ 1
Cryptography 1
Federated Learning 2
Goa入门 1
Java 2
LeetCode 59
Leetcode 1
Mac终端命令 1
Swagger 1
coding 9
data 1
encryption 1
github 1
golang 1
hexo 2
important 1
intro 1
npm 1
paper 2
paper reading 1
paperReading 2
python转换 1
pytorch学习 2
云端学习笔记 1
代码 2
入门 5
入门指引 1
刷题 2
双指针 1
基础 2
大数据，spark 1
排序 1
提升自我 1
深度学习 1
神经网络搜索 2
禅 1
编程 8
编程技巧， 1
联合学习 3
自我修炼 1
论文阅读 1
配置文件 1

Recientes

Archivos

Etiquetas

AI 1
BigData 1
C++ 1
Cryptography 1
Federated Learning 2
Goa入门 1
Java 2
LeetCode 59
Leetcode 1
Mac终端命令 1
Swagger 1
coding 9
data 1
encryption 1
github 1
golang 1
hexo 2
important 1
intro 1
npm 1
paper 2
paper reading 1
paperReading 2
python转换 1
pytorch学习 2
云端学习笔记 1
代码 2
入门 5
入门指引 1
刷题 2
双指针 1
基础 2
大数据，spark 1
排序 1
提升自我 1
深度学习 1
神经网络搜索 2
禅 1
编程 8
编程技巧， 1
联合学习 3
自我修炼 1
论文阅读 1
配置文件 1
Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×